Harmonic price patterns identify the stages of a retracement so that when the pattern is complete, you have a clear buy or sell signal. Retracements are vexing at all times and any help is always welcome, although with harmonic price patterns, the orthodoxy is to apply Fibonacci numbers. Again, Fibonacci numbers are not a proven theory and in fact there is a great deal of evidence that Fibonacci numbers appear in securities prices, including Forex, only about the number of times as chance would allow. Nevertheless, when a perfect or near-perfect Fibonacci number does appear, plenty of traders will see it and produce the expected outcome, so it does not pay to dismiss Fibonacci-based trading ideas out of hand.
Note that harmonic price patterns are unrelated to classic chart patterns (head-and-shoulders, double top, et al.). The key books on harmonics are by Scott Carney, author of The Harmonic Trader (1999) and Harmonic Trading of the Financial Markets, Volumes 1 and 2 (2010). Harmonics have become increasingly popular in Forex in recent years, and specialized software is now available. Like all trading concepts based on Fibonacci numbers, harmonic pattern identification takes a lot of practice and a lot of re-drawing and re-calculation, since the numbers so seldom hit exactly where they are supposed to. However, a focus on retracements can be helpful in improving trading performance, since retracements are where most losses are clustered.
It may be of interest that some people can “see” harmonic patterns and others cannot, even with the help of software that does the hard work of performing the calculations. Proponents of harmonic patterns claim that they appear hundreds of times per day and thousands of time per week, but if that were true, you should be able to pick any chart on any timeframe and find one of the seven or eight standard harmonic patterns within seconds. We can find every other technical phenomenon with no effort at all, on any chart, but not harmonic patterns. Therefore, the illustration here has to be a model. See the figure below. It is the basic ABCD pattern and here is the “Gartley bearish pattern.” Other patterns are variations of this core concept, including the Bat, Butterfly, Crab, and Shark patterns. Note that the Gartley pattern is named after H.M. Gartley, who wrote a book titled Profits in the Stock Market in 1935. Gartley did not use Fibonacci numbers although he identified the sequence of price moves.
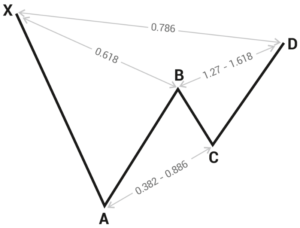
Gartley’s observations are valid no matter how long ago they were made. Gartley pointed out that an extreme short-term move (like X to A) is usually followed by a lesser correction (B to C). This correction occurs when demand dries up — everyone who was going to buy has already bought. But if the security is now a “bargain” in some sense, earlier buyers will return to the market, leading to the rise from C to D. If the move fizzles at D before it gets to the highest high at X, the bounce is over. The market psychology is obvious and the moves can be explained in terms of supply and demand.
Harmonic pattern proponents add Fibonacci numbers to the basic move-correction-resumed-move model. The key principle is that a big move down from X will retrace by 61.8% from A to B. It will then pull back again to a lower low at point C by 38%. After that it will rise to point D, and in the absence of matching-and-surpassing point X, becomes bearish. You become a seller at point D. The problem is that quite frequently, after a pullback from point D, the price goes on to a higher high.
It is certainly true that we get a lot of A to B moves that measure 61.8%. But the number of times that we then get a B to C move by 38% is limited. Note that the harmonic pattern rule is that failure to match-and-surpass the starting point high is a bearish signal regardless of whatever pattern came between point X and point D.

